[Data Structure] 힙 (Heap)

들어가기 전

우선순위 큐를 위해 만들어진 자료 구조인 만큼, 우선순위 큐에 대한 개념을 먼저 잡고 들어간다.

우선순위 큐 (Priority Queue)

우선순위의 개념을 큐에 도입한 자료 구조이다.

특징으로는 데이터들이 우선순위를 가지고 있고, 우선순위가 높은 데이터가 먼저 나간다.

• 각 자료 구조의 먼저 데이터가 삭제되는 요소 비교

  자료 구조	삭제되는 요소
  스택 (Stack)	가장 최근에 들어온 데이터
  큐 (Queue)	가장 먼저 들어온 데이터
  우선순위 큐 (Priority Queue)	가장 우선순위가 높은 데이터

  스택과 큐에 대해서는 #Stack VS Queue 게시글 참고

• 우선순위 큐의 이용 사례

  • 시뮬레이션 시스템
  • 네트워크 트래픽 제어
  • 운영 체제에서의 작업 스케쥴링
  • 수치 해석적인 계산

우선순위 큐는 배열, 연결 리스트, 힙으로 구현이 가능하며, 이 중 힙(Heap)으로 구현하는 것이 가장 효율적이다.

우선순위 큐를 구현하는 표현 방법	삽입	삭제
순서 없는 배열	$O(1)$	$O(n)$
순서 없는 연결 리스트	$O(1)$	$O(n)$
정렬된 배열	$O(n)$	$O(1)$
정렬된 연결 리스트	$O(n)$	$O(1)$
힙 (Heap)	$O(log \ n)$	$O(log \ n)$

힙(Heap)의 개념

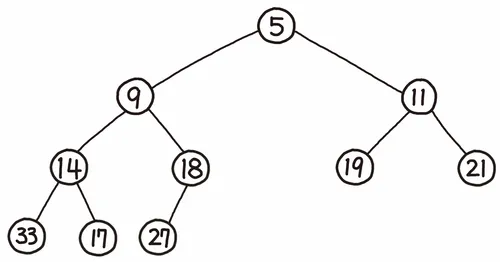
완전 이진 트리의 일종으로, 우선순위 큐를 위해 만들어진 자료 구조로,

여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료 구조이다.

힙은 일종의 반정렬 상태(느슨한 정렬 상태)를 유지한다.

• 큰 값이 상위 레벨에 있고, 작은 값이 하위 레벨에 있다는 정도를 의미한다.
• 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.

힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

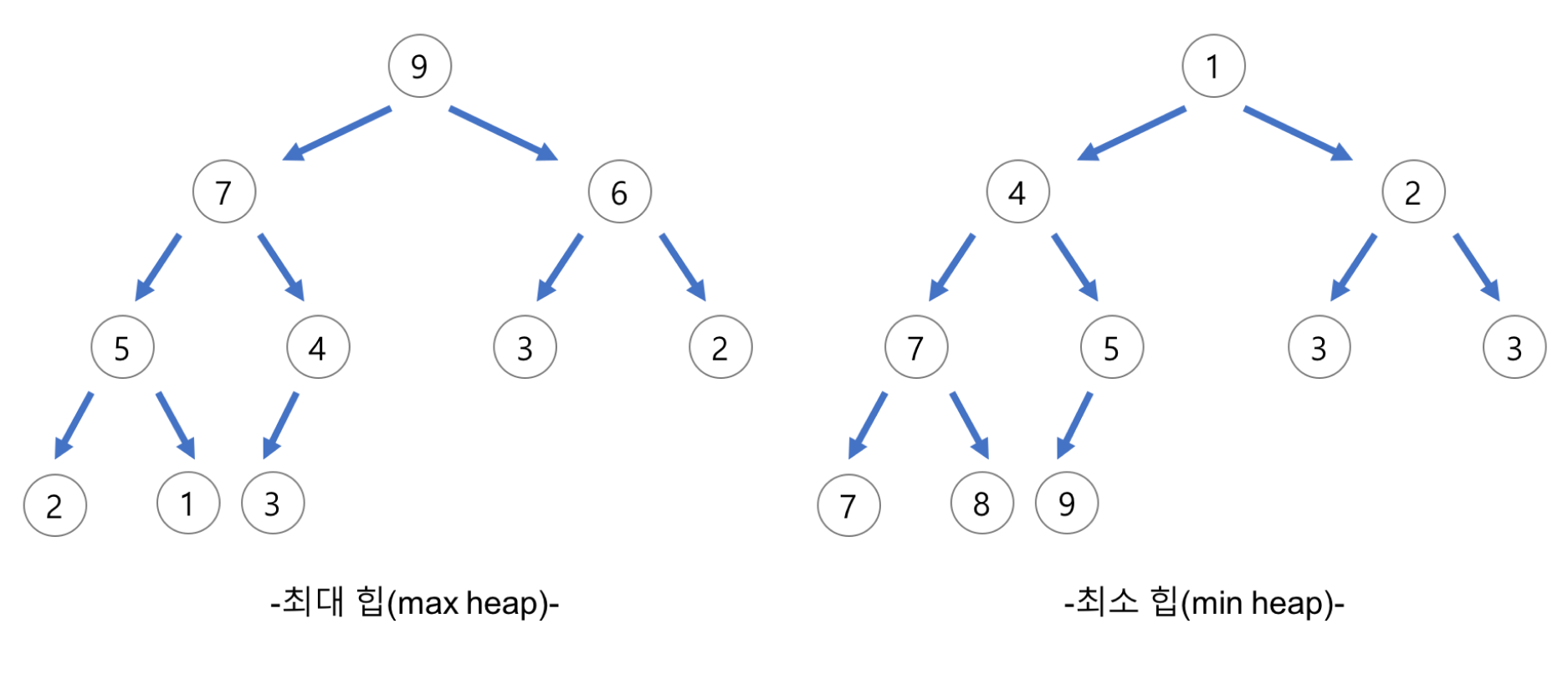
힙(Heap)의 종류

• 최대 힙 (Max Heap)

  부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리

  $key(부모 \ 노드) \geq key(자식 \ 노드)$

• 최소 힙 (Min Heap)

  부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리

  $key(부모 \ 노드) \leq key(자식 \ 노드)$

힙(Heap)의 구현

해당 게시글에서는 TypeScript를 이용해 힙을 구현할 예정이다.

예제 코드 1 (Min Heap)

힙(Heap) 클래스 초기화

최소 힙의 부모와 자식 간에 다음과 같은 관계가 성립한다.

• 왼쪽 자식의 index = $부모의 \ index \times 2 + 1$
• 오른쪽 자식의 index = $(부모의 \ index \times 2) + 2$
• 부모의 index = $\frac{자식의 \ 인덱스 - 1}{2}$

/heap_exmaple/min_heap.ts

class MinHeap {
  heap: Array<number | string>;

  constructor() {
    // 힙 저장할 배열
    this.heap = [];
  }

  // 힙의 크기를 반환하는 메서드
  size(): number {
    return this.heap.length;
  }

  // 두 값을 바꿔주는 메서드
  swap(idx_1: number, idx_2: number): void {
    [this.heap[idx_1], this.heap[idx_2]] = [this.heap[idx_2], this.heap[idx_1]];
  }
}

힙(Heap)의 삽입 연산

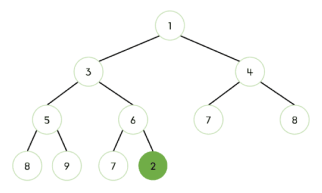
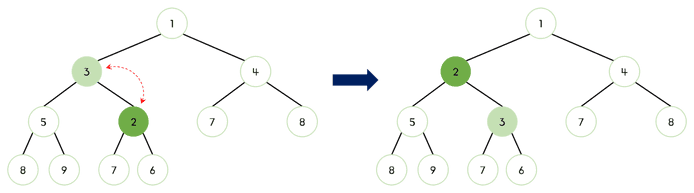
최소 힙의 삽입 연산(Bubble Up¹)은 다음과 같은 단계로 이루어진다.

1. 힙의 마지막 위치에 요소를 추가한다.
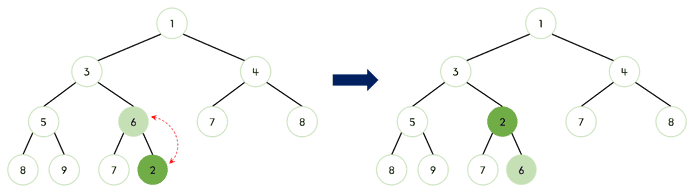
2. 새로운 요소를 추가한 위치에서부터, 부모 노드와 새로 추가된 노드의 값을 비교한다.
   • 만약 새로 추가된 노드의 값이 부모 노드의 값보다 작다면, 부모 노드와 새로 추가된 노드의 위치를 교환한다.
3. 이전 단계에서 교환된 새로 추가된 노드와 부모 노드의 값 비교를 반복한다.
   • 이 단계를 반복하여 최소 힙의 규칙을 지키도록 한다.

이미지로 보기

1. 먼저 힙의 마지막 노드로 새로운 요소 2를 삽입한다.

2. 부모 노드 6과 비교했을 때, 2가 작으므로 교체한다.

3. 부모 노드 3과 비교했을 때, 2가 작으므로 교체한다.
4. 부모 노드 1과 비교했을 때, 2가 크므로 더 이상 교체하지 않는다.

/heap_exmaple/min_heap.ts

// 새로운 노드를 추가하는 메서드
add(value: number) {
  this.heap.push(value); // 힙의 끝에 새로운 노드 추가
  this.bubbleUp(); // 새로운 값이 추가된 위치에서 bubbleUp() 수행
}

bubbleUp(): void {
  let index = this.heap.length - 1; // 새로운 노드가 추가된 위치
  let parentIdx = Math.floor((index - 1) / 2); // 부모 노드의 위치

  while (
    this.heap[parentIdx] && // 부모 노드가 존재하고
    this.heap[index][1] < this.heap[parentIdx][1] // 새로운 노드가 부모 노드보다 작은 경우
  ) {
    this.swap(index, parentIdx); // 두 노드의 값을 교체
    index = parentIdx; // 인덱스를 부모 노드의 인덱스로 변경
    parentIdx = Math.floor((index - 1) / 2); // 새로운 부모 노드의 인덱스 계산
  }
}

힙(Heap)의 삭제 연산

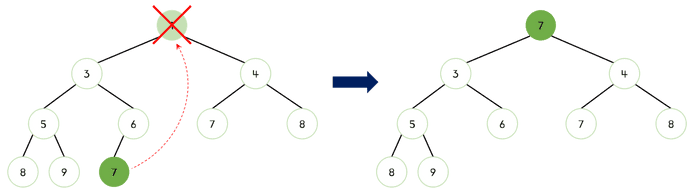
최소 힙의 삭제 연산(Bubble Down²)은 다음과 같은 단계로 이루어진다.

1. 힘에서 가장 작은 값을 가진 노드를 제거한다.
   • 이때, 최소 힙에서 가장 작은 값은 루트 노드이다.
2. 힙의 맨 마지막에 있는 노드를 새로운 루트 노드로 이동시킨다.
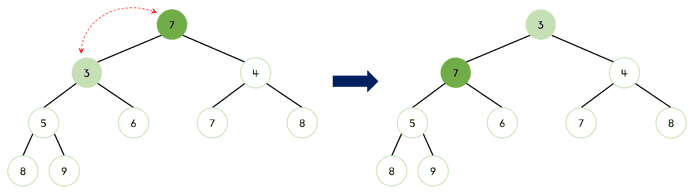
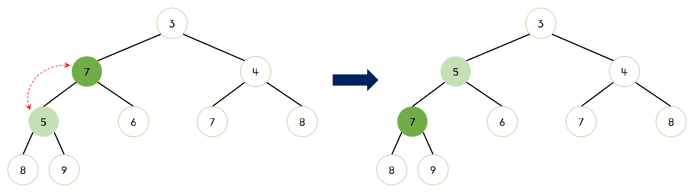
3. 새로운 루트 노드와 자식 노드의 값을 비교하여, 자식 노드의 값이 작다면, 루트 노드의 위치를 교환한다.
4. 이전 단계에서 교환된 새로운 루트 노드와 자식 노드의 값 비교를 반복한다.
   • 이 단계를 반복하여 최소 힙의 규칙을 지키도록 한다.

이미지로 보기

1. 먼저 루트 노드가 삭제되며, 빈 루트 노드 자리에는 힙의 마지막 노드 7을 가져온다.

2. 새로운 루트 노드인 7과 자식 노드들을 비교했을 때, 7이 더 크므로 교체되어야 한다. 이때, 자식 노드 중 더 작은 값인 3과 7이 교체된다.

3. 7이 아직 자식 노드들보 더 크기 때문에 교체되어야 한다. 이때, 자식 노드 중 더 작은 값인 5와 7이 교체된다.
4. 7이 자식 노드들보다 작으므로 더 이상 교체하지 않는다.

/heap_exmaple/min_heap.ts

poll(): number {
  if (this.add.length === 1) {
    return this.heap.pop() as number; // 힙의 크기가 1인 경우, 힙에서 값을 삭제하고 return
  }

  const value = this.heap[0]; // 힙의 최솟값(루트 노드의 값)을 저장
  this.heap[0] = this.heap.pop() as number; // 힙의 끝에 있는 값을 루트 노드로 이동
  this.bubbleDown(); // 루트 노드에서 buubleDown을 수행
  return value; // 삭제한 최솟값 return
}

bubbleDown(): void {
  let index = 0;
  let leftIdx = index * 2 + 1;
  let rightIdx = index * 2 + 2;

  while (
    // 왼쪽 자식 노드가 존재하면서 값이 루트 노드보다 작거나
    (this.heap[leftIdx] && this.heap[leftIdx][1] < this.heap[index][1]) ||
    // 오른쪽 자식 노드가 존재하면서 값이 루트 노드보다 작은 경우
    (this.heap[rightIdx] && this.heap[rightIdx][1] < this.heap[index][1])
  ) {
    let smallerIdx = leftIdx; // 왼쪽 자식 노드가 더 작다고 가정
    if (
      this.heap[rightIdx] &&
      this.heap[rightIdx][1] < this.heap[smallerIdx][1] // 오른쪽 자식 노드가 존재하면서 더 작다면
    ) {
      smallerIdx = rightIdx; // 오른쪽 자식 노드의 index로 변경
    }

    this.swap(index, smallerIdx); // 두 노드의 값을 교체
    index = smallerIdx; // index를 더 작은 값의 자식 노드의 index로 변경
    leftIdx = index * 2 + 1; // 왼쪽 자식 노드의 index 계산
    rightIdx = index * 2 + 2; // 오른쪽 자식 노드의 index 계산
  }
}

힙(Heap)의 구현 전체 코드

/heap_exmaple/min_heap.ts

class MinHeap {
  heap: number[];

  constructor() {
    // 힙 저장할 배열
    this.heap = [];
  }

  // 힙의 크기를 반환하는 메서드
  size(): number {
    return this.heap.length;
  }

  // 두 값을 바꿔주는 메서드
  swap(idx_1: number, idx_2: number): void {
    [this.heap[idx_1], this.heap[idx_2]] = [this.heap[idx_2], this.heap[idx_1]];
  }

  // 새로운 노드를 추가하는 메서드
  add(value: number) {
    this.heap.push(value); // 힙의 끝에 새로운 노드 추가
    this.bubbleUp(); // 새로운 값이 추가된 위치에서 bubbleUp() 수행
  }

  bubbleUp(): void {
    let index = this.heap.length - 1; // 새로운 노드가 추가된 위치
    let parentIdx = Math.floor((index - 1) / 2); // 부모 노드의 위치

    while (
      this.heap[parentIdx] && // 부모 노드가 존재하고
      this.heap[index][1] < this.heap[parentIdx][1] // 새로운 노드가 부모 노드보다 작은 경우
    ) {
      this.swap(index, parentIdx); // 두 노드의 값을 교체
      index = parentIdx; // 인덱스를 부모 노드의 인덱스로 변경
      parentIdx = Math.floor((index - 1) / 2); // 새로운 부모 노드의 인덱스 계산
    }
  }

  poll(): number {
    if (this.add.length === 1) {
      return this.heap.pop() as number; // 힙의 크기가 1인 경우, 힙에서 값을 삭제하고 return
    }

    const value = this.heap[0]; // 힙의 최솟값(루트 노드의 값)을 저장
    this.heap[0] = this.heap.pop() as number; // 힙의 끝에 있는 값을 루트 노드로 이동
    this.bubbleDown(); // 루트 노드에서 buubleDown을 수행
    return value; // 삭제한 최솟값 return
  }

  bubbleDown(): void {
    let index = 0;
    let leftIdx = index * 2 + 1;
    let rightIdx = index * 2 + 2;

    while (
      // 왼쪽 자식 노드가 존재하면서 값이 루트 노드보다 작거나
      (this.heap[leftIdx] && this.heap[leftIdx][1] < this.heap[index][1]) ||
      // 오른쪽 자식 노드가 존재하면서 값이 루트 노드보다 작은 경우
      (this.heap[rightIdx] && this.heap[rightIdx][1] < this.heap[index][1])
    ) {
      let smallerIdx = leftIdx; // 왼쪽 자식 노드가 더 작다고 가정
      if (
        this.heap[rightIdx] &&
        this.heap[rightIdx][1] < this.heap[smallerIdx][1] // 오른쪽 자식 노드가 존재하면서 더 작다면
      ) {
        smallerIdx = rightIdx; // 오른쪽 자식 노드의 index로 변경
      }

      this.swap(index, smallerIdx); // 두 노드의 값을 교체
      index = smallerIdx; // index를 더 작은 값의 자식 노드의 index로 변경
      leftIdx = index * 2 + 1; // 왼쪽 자식 노드의 index 계산
      rightIdx = index * 2 + 2; // 오른쪽 자식 노드의 index 계산
    }
  }
}

예제 코드 2 (Min Heap & Max Heap)

기본 힙 (Heap)

/heap_exmaple/heap.ts

class Heap {
  items: number[];
  constructor() {
    this.items = [];
  }

  // 값을 서로 바꾸는 메서드
  swap(index_1: number, index_2: number): void {
    let temp = this.items[index_1]; // items의 index_1의 값을 temp(임시공간)에 담기
    this.items[index_1] = this.items[index_2]; // index_1에 index_2의 값을 저장
    this.items[index_2] = temp; // index_2에 아까 index_1의 값을 temp에 넣어놓은 값을 저장
  }

  // 부모 인덱스 구하는 메서드
  parentIndex(index: number): number {
    return Math.floor((index - 1) / 2);
  }

  // 왼쪽 자식 인덱스 구하는 메서드
  leftChildIndex(index: number): number {
    return index * 2 + 1;
  }

  // 오른쪽 자식 인덱스 구하는 메서드
  rightChildIndex(index: number): number {
    return index * 2 + 2;
  }

  // 부모 노드 구하는 메서드
  parent(index: number): number {
    return this.items[this.parentIndex(index)];
  }

  // 왼쪽 자식 노드 구하는 메서드
  leftChild(index: number): number {
    return this.items[this.leftChildIndex(index)];
  }

  // 오른쪽 자식 노드 구하는 메서드
  rightChild(index: number): number {
    return this.items[this.rightChildIndex(index)];
  }

  // 최대 힙의 경우 최댓값을 반환,
  // 최소 힙의 경우 최솟값을 반환하는 메서드
  peek(): number {
    return this.items[0];
  }

  // 힙의 크기(항목 개수)를 반환하는 메서드
  size(): number {
    return this.items.length;
  }
}

export default Heap;

최소 힙 (Min Heap)

MinHeap 클래스는 Heap 클래스를 상속받았으므로, Heap 클래스의 메소드를 모두 사용할 수 있음

/heap_exmaple/min_heap.ts

import Heap from "./heap";

class MinHeap extends Heap {
  bubbleUp(): void {
    let index = this.items.length - 1;

    while (
      this.parent(index) !== undefined &&
      this.parent(index) > this.items[index]
    ) {
      this.swap(index, this.parentIndex(index));
      index = this.parentIndex(index);
    }
  }

  bubbleDown(): void {
    let index = 0;

    while (
      this.leftChild(index) !== undefined &&
      (this.leftChild(index) < this.items[index] ||
        this.rightChild(index) < this.items[index])
    ) {
      let smallerIndex: number = this.leftChildIndex(index);

      if (
        this.rightChild(index) !== undefined &&
        this.rightChild(index) < this.items[smallerIndex]
      ) {
        smallerIndex = this.rightChildIndex(index);
      }

      this.swap(index, smallerIndex);
      index = smallerIndex;
    }
  }

  // 힙의 원소를 추가하는 함수
  add(item: number): void {
    this.items[this.items.length] = item;
    this.bubbleUp();
  }

  // 힙에서 원소를 빼내는 함수
  // 최소 힙이라면 최솟값이 빠져나오고,
  // 최대 힙이라면 최댓값이 빠져나온다.
  poll(): number {
    let item = this.items[0]; // 첫번째 원소 keep

    this.items[0] = this.items[this.items.length - 1]; // 맨 마지막 원소를 첫 번째 원소로 복사
    this.items.pop() as number; // 맨 마지막 원소 삭제
    this.bubbleDown();

    return item; // keep 해둔 값 반환
  }
}

export default MinHeap;

최대 힙 (Max Heap)

MaxHeap 클래스는 MinHeap 클래스를 상속받았으므로, MinHeap 클래스의 메소드를 모두 사용할 수 있지만, bubbleUp과 bubbleDown 에서드는 Overriding(재정의)함

/heap_exmaple/max_heap.ts

import MinHeap from "./min_heap";

class MaxHeap extends MinHeap {
  bubbleUp(): void {
    let index = this.items.length - 1;
    while (
      this.parent(index) !== undefined &&
      this.parent(index) < this.items[index]
    ) {
      this.swap(index, this.parentIndex(index));
      index = this.parentIndex(index);
    }
  }

  bubbleDown(): void {
    let index = 0;

    while (
      this.leftChild(index) !== undefined &&
      (this.leftChild(index) > this.items[index] ||
        this.rightChild(index) > this.items[index])
    ) {
      let largerIndex = this.leftChildIndex(index);

      if (
        this.rightChild(index) !== undefined &&
        this.rightChild(index) > this.items[largerIndex]
      ) {
        largerIndex = this.rightChildIndex(index);
      }

      this.swap(largerIndex, index);
      index = largerIndex;
    }
  }
}

export default MaxHeap;

실행 결과

실행 코드

/heap_exmaple/client.ts

import MaxHeap from "./max_heap";
import MinHeap from "./min_heap";

const exampleArray: number[] = [1, 10, 5, 100, 8, 3, 4, 76, 32, 44, 178];

const stopPoint: number = 5;

const minheap = new MinHeap();
const maxheap = new MaxHeap();

const Client = (heap: MinHeap | MaxHeap, heapName: string) => {
  const pollArray: number[] = [];

  exampleArray.map((item: number) => {
    heap.add(item);
  });

  console.log(`${heapName}'s Items: ${heap.items.toString()}`);

  for (let i = 0; i < stopPoint; i++) {
    pollArray.push(heap.poll());
  }

  console.log(`${heapName}'s delete Items: ${pollArray.toString()}`);
  console.log(`After delete, ${heapName}'s Items: ${heap.items.toString()}`);
  console.log("");
};

Client(minheap, "MinHeap");
Client(maxheap, "MaxHeap");

결과값

MinHeap's Items: 1,8,3,32,10,5,4,100,76,44,178
MinHeap's delete Items: 1,3,4,5,8
After delete, MinHeap's Items: 10,32,44,178,100,76

MaxHeap's Items: 178,100,5,32,76,3,4,1,10,8,44
MaxHeap's delete Items: 178,100,76,44,32
After delete, MaxHeap's Items: 10,8,5,1,4,3

참고 사이트

heejeong Kwon - [자료구조] 힙(heap)이란

chamdom.blog - [자료구조] JavaScript로 힙(Heap) 구현하기

냥인의 블로그 - [자바스크립트 자료구조] 힙(Heap) - (1) 최소힙, 최대힙 구현

---

1. 힙에 값을 삽입할 때, 부모와 비교해서 정렬이 필요하면(최소 힙의 경우, 부모가 자신보다 크면 / 최대 힙의 경우, 부모가 자신보다 작으면) 부모와 값을 교환해서 올바르게 정렬이 될 때 까지 올라가는 것을 Bubble Up이라고 한다. ↩︎

2. 루트 노드를 삭제한 다음, 마지막 노드를 루트로 올리고, 루트 노드와 아래 자식 노드들과의 값을 비교하여 값이 크거나 작으면 (최소 힙의 경우, 자식이 자신보다 값이 작으면 / 최대 힙의 경우, 자식이 자신보다 크면) 자식과 값을 교환해서 올바르게 정렬이 될 때 까지 내려가는 것을 Bubble Down이라고 한다. ↩︎