[Data Structure] 트리 (Tree)

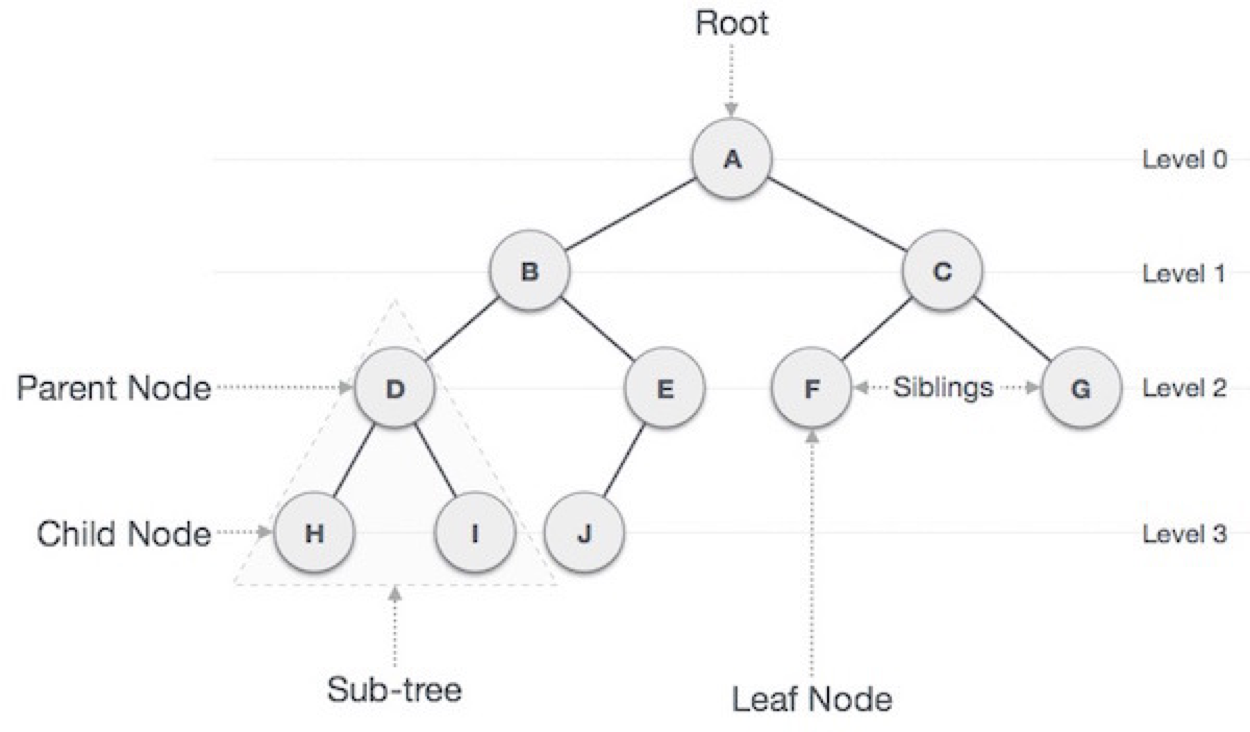
트리(Tree)의 개념

트리는 노드로 이루어진 자료 구조이다.

트리의 특징을 정리하자면,

1. 트리는 하나의 루트 노드를 갖는다.
2. 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
3. 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.

이러한 특징을 갖고 있으며,

노드(node)들과 노드들을 연결하는 간선(edge)들로 구성되어 있다.

• 트리에는 사이클(cycle)이 존재할 수 없고,
• 노드들은 특정 순서로 나열될 수도 있고, 그렇지 않을 수도 있으며,
• 각 노드는 어떤 자료형으로도 표현이 가능하다.

class Node {
  public name: string;
  public children: Node[];
}

또한 트리는 비선형 자료 구조로 계층적 관계를 표현한다.

ex) 디텍토리 구조, 조직도 등…

자료 구조인 #그래프(Graph)의 한 종류로,

• 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)이며,
• 또는 DAG¹의 한 종류이다.

트리(Tree)의 특징

• 그래프의 한 종류로써, 최소 연결 트리라고도 불린다.
• 트리는 계층 모델이다.
• DAG¹의 한 종류이다.
  • loop나 circuit가 없으며, 당연히 self-loop도 없다.
  • 즉, 사이클이 존재하지 않는다.
• 노드가 $n$개인 트리는 항상 $n - 1$개의 간선(edge)을 가진다.
  • 즉, 간선은 항상 $(정점의 \ 개수 - 1)$만큼을 가진다.
• 루트에서 어떤 노드로 가는 경로는 유일하다.
  • 임의의 두 노드 간의 경로도 유일하다.
  • 즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
• 한 개의 루트 노드만이 존재하며, 모든 자식 노드는 한 개의 부모 노드만을 가진다.
  • 부모-자식 관계이므로 흐름은 top-bottom 또는 bottom-top으로 이루어진다.
• 순회는 Pre-order, In-order 또는 Post-order로 이루어지며, 이 3가지 모두 DFS² / BFS³ 안에 있다.
• 트리는 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대 힙, 최소 힙) 등이 있다.

트리(Tree)의 종류

이진 트리 VS 이진 탐색 트리

• 이진 탐색 트리 (Bianary Search Tree)

  모든 노드가 아래와 같은 특정 순서를 따르는 속성이 있는 이진 트리이다.

  $모든 \ 왼쪽 \ 자식들 \leq n < 모든 \ 오른쪽 \ 자식들$ (모든 노드 $n$에 대해서 반드시 참)

균형 트리 VS 비균형 트리

• 균형 트리

  $O(log\,n)$시간에 insert와 find를 할 수 있을 정도로 균형이 잘 잡혀있는 경우를 말한다.

  ex) red-black 트리, AVL 트리

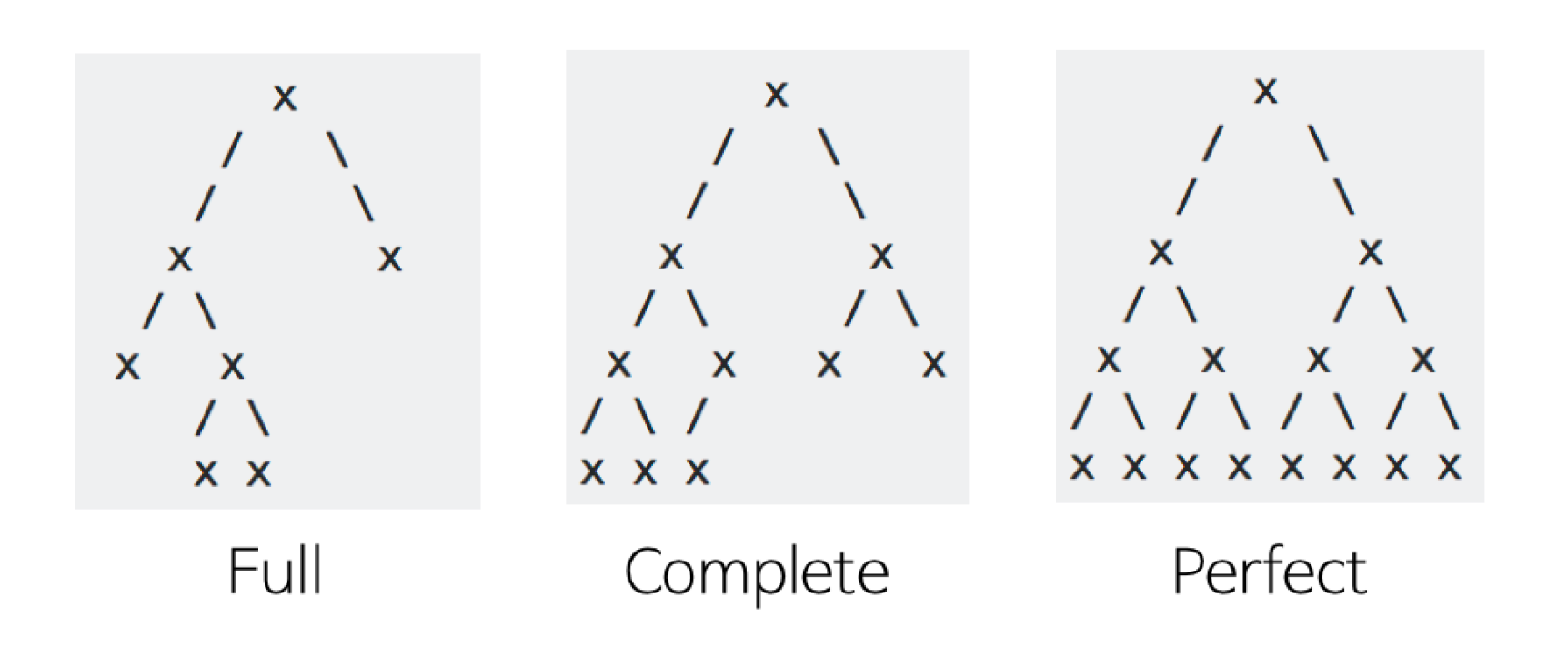
완전 이진 트리 VS 전 이진 트리 VS 포화 이진 트리

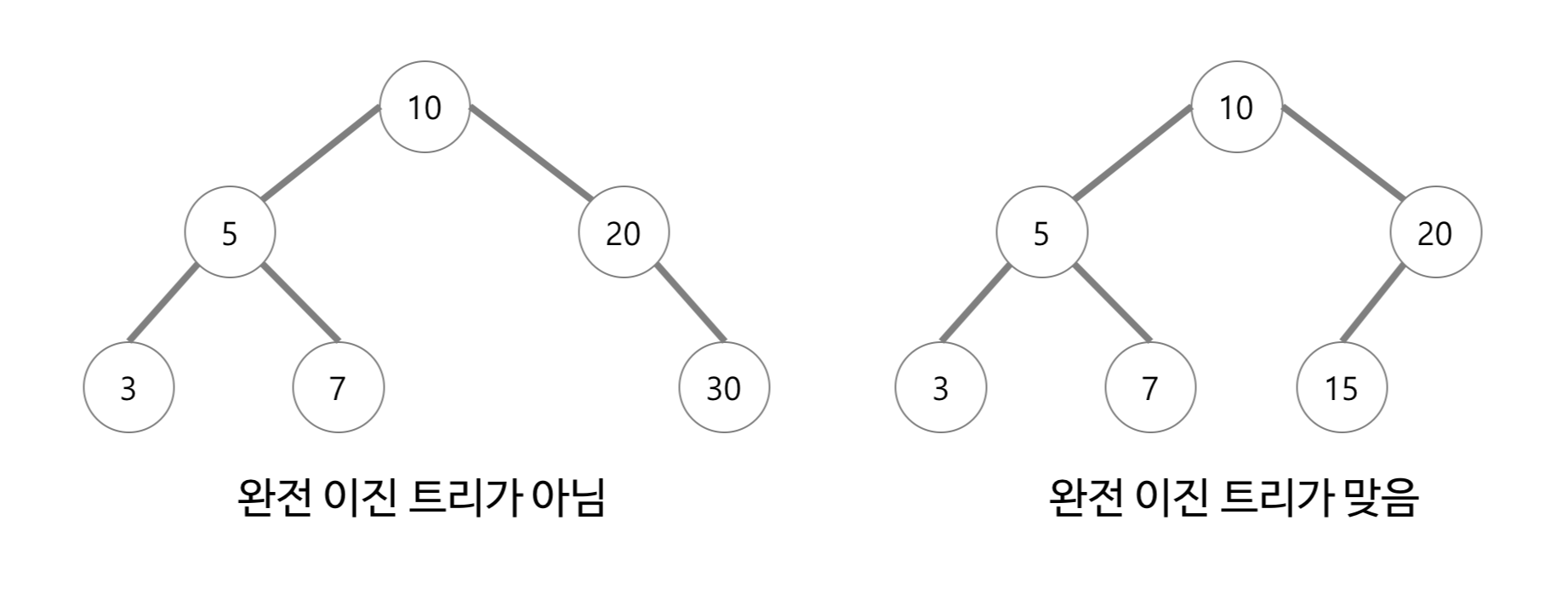
완전 이진 트리

• 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리를 말한다.
  • 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
• 마지막 레벨은 꽉 차 있지 않아도 되지만, 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
  • 마지막 레벨 $h$에서 1 ~ $2h - 1$개의 노드를 가질 수 있다.
• 또 다른 정의는 가장 오른쪽의 잎 노드가 (아마도 모두) 제거된 포화 이진 트리이다.
• 완전 이진 트리는 배열을 사용해 효율적으로 표현이 가능하다.

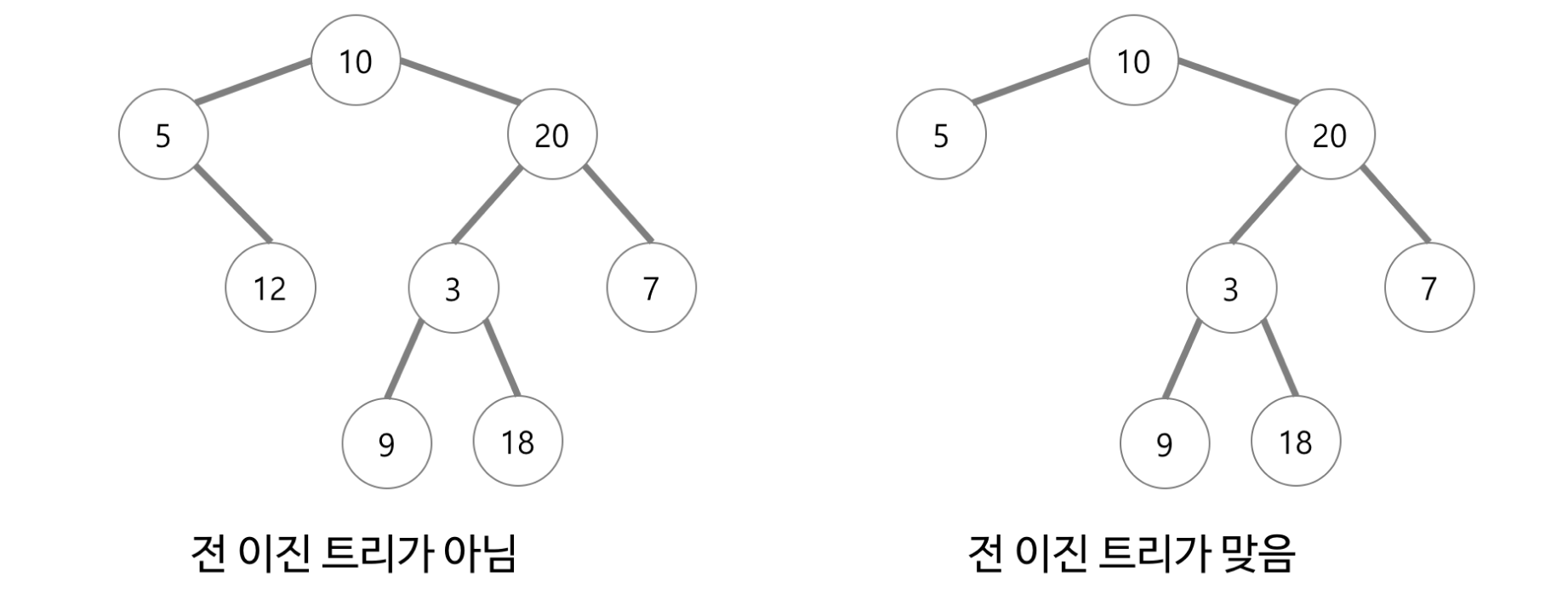
전 이진 트리

• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리를 말한다.

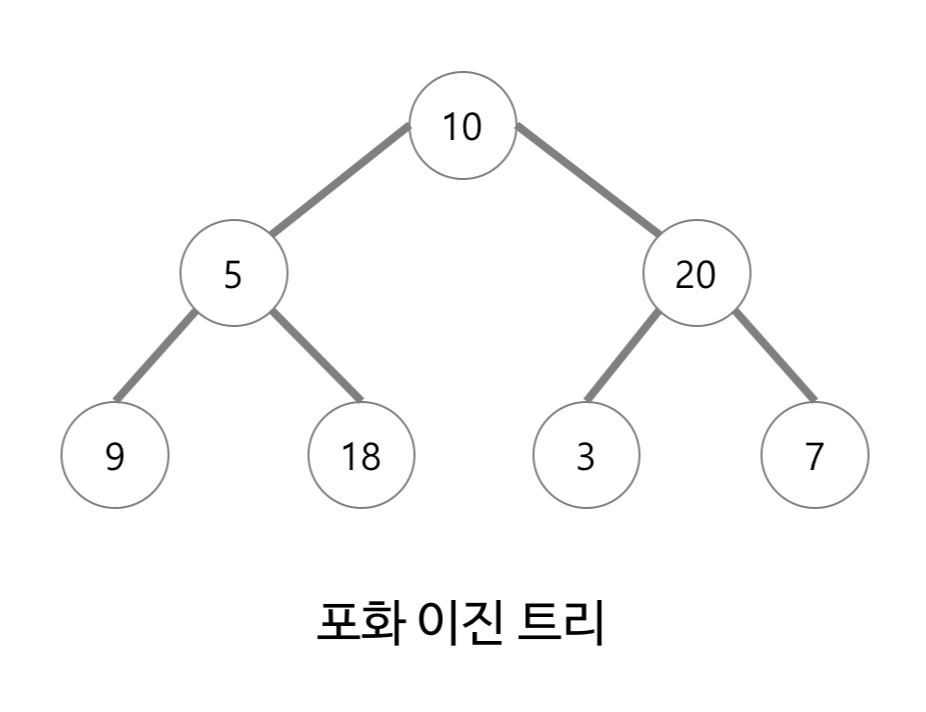
포화 이진 트리

• 전 이진 트리이면서 완전 이진 트리인 경우를 말한다.
• 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
  • 즉, 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
• 모든 내부 노드가 두 개의 자식 노드를 가진다.
• 노드의 개수가 정확히 $2^{k-1}$개($k$ : 트리의 높이)여야 하며, 흔하게 나타나는 경우는 아니다.
  • 즉, 이진 트리가 모두 포화 이진 트리일 것이라고 생각해서는 안된다.

이진 힙 (최소 힙과 최대 힙)

• 최소 힙 (Min Heap)

  트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있는 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다.

  • 즉, $key(부모 \ 노드) \geq key(자식 \ 노드)$인 완전 이진 트리

  • 가장 큰 값은 루트 노드이다.

  • $n$개가 힙에 들어가 있으면, 높이는 $log(n)$이다.

• 최대 힙 (Max Heap)

  원소가 내림차순으로 정렬되어 있다는 점에서만 최소 힙과 다르다.

  각 노드의 원소가 자식들의 원소보다 크다.

• #힙 (Heap) 게시글 참고

트라이 (Trie)

접두사 트리(Prefix Tree)라고도 부른다.

• n-차 트리(n-ary Tree)⁴의 변종이다.
• 각 노드에 문자를 저장하는 자료 구조이다.
  • 따라서, 트리를 아래쪽으로 순회하면 단어 하나가 나온다.
• 접두사를 빠르게 찾아보기 위한 흔한 방식으로, 모든 언어를 트라이에 저장해 놓는 방식이 있다.
  • 이러한 방식으로 인해, 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.

트리(Tree)의 구현 방법

기본적으로 트리는 그래프의 한 종류이므로,

그래프의 구현 방법(#인접 리스트 또는 인접 배열)으로 구현할 수 있다.

인접 배열 이용

• 1차원 배열에 자신의 부모 노드만 저장하는 방법

  트리는 부모 노드를 0개 또는 1개를 가지기 때문

  부모 노드를 0개 : 루트 노드

• 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법

  이진 트리는 각 노드가 최대 두 개의 자식을 갖는 트리이기 때문

  ex) A[i][0] : 왼쪽 자식 노드, A[i][1] : 오른쪽 자식 노드

인접 리스트 이용

• 가중치가 없는 트리의 경우

  ArrayList< ArrayList > list = new ArrayList<>();
  

• 가중치가 있는 트리의 경우

  class Node {
    int num, dist; // 노드 번호, 거리
  }
  
  int "정점의 수"
  
  ArrayList[] list = new ArrayList["정점의 수" + 1]
  

같이 보기

트리(Tree)와 관련된 용어

• 루트 노드 (Root Node)

  부모가 없는 노드로, 트리는 하나의 루트 노드만을 가진다.

• 단말 노드 (Leaf Node)

  자식이 없는 노드로, ‘말단 노드’ 또는 ‘잎 노드’라고도 불린다.

• 내부(Internal) 노드

  단말 노드가 아닌 노드

• 간선 (Edge)

  노드를 연결하는 선 (Link, Branch라고도 부름)

• 형제 (Sibling)

  같은 부모를 가지는 노드

• 노드의 크기 (Size)

  자신을 포함한 모든 자손 노드의 개수

• 노드의 깊이 (Depth)

  루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수

• 노드의 레벨 (Level)

  트리의 특정 깊이를 가지는 노드의 집합

• 노드의 차수 (Degree)

  $ \frac{하위 \ 트리 \ 개수}{간선 \ 수 (degree)} = 각 \ 노드가 \ 지닌 \ 가지의 \ 수$

• 트리의 차수 (Degree of Tree)

  트리의 최대 차수

• 트리의 높이 (Height)

  루트 노드에서 가장 깊숙히 있는 노드의 깊이

그래프(Graph)와 트리(Tree)의 차이

정의

• 그래프 (Graph)

  노드(node)와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 자료 구조

• 트리 (Tree)

  DAG¹의 그래프의 한 종류

방향성

• 그래프 (Graph)

  방향 그래프(Directed)와 무방향 그래프(Undirected) 모두 존재

• 트리 (Tree)

  방향 그래프(Directed)

사이클

• 그래프 (Graph)

  사이클(Cycle)과 자체 간선(self-loop) 모두 가능하며, 순환 그래프(Cyclic)와 비순환 그래프(Acyclic) 모두 존재

• 트리 (Tree)

  사이클(Cycle)과 자체 간선(self-loop) 모두 불가능하며, 비순환 그래프(Acyclic)

루트 노드

• 그래프 (Graph)

  루트 노드의 개념이 없음

• 트리 (Tree)

  한 개의 루트 노드만이 존재하며, 모든 자식 노드는 한개의 부모 노드만을 가짐

부모-자식

• 그래프 (Graph)

  부모-자식의 개념이 없음

• 트리 (Tree)

  부모- 자식 관계가 존재하며, top-bottom 또는 bottom-top으로 이루어짐

모델

• 그래프 (Graph)

  네트워크 모델

• 트리 (Tree)

  계층 모델

순회

• 그래프 (Graph)

  DFS², BFS³

• 트리 (Tree)

  DFS²와 BFS³안의 Pre-, In-, Post-order

간선의 수

• 그래프 (Graph)

  그래프에 따라 간선의 수가 다르며, 간선이 없을 수도 있음

• 트리 (Tree)

  노드가 $n$인 트리는 항상 $n-1$의 간선을 가짐

경로

• 그래프 (Graph)

  -

• 트리 (Tree)

  임의의 두 노드 간의 경로는 유일

예시 및 종류

• 그래프 (Graph)

  지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수 과목 등…

• 트리 (Tree)

  이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대 힙, 최소 힙) 등…

참고 사이트

heejeong Kwon - [자료 구조] 트리(Tree)란

COCO-STUDY - Part 1. 데이터 구조 - 트리 데이터 구조

---

1. Directed Acyclic Graph, 방향성이 있는 비순환 그래프 ↩︎ ↩︎² ↩︎³

2. Depth First Search, 깊이 우선 탐색 ↩︎ ↩︎² ↩︎³

3. Breadth First Search, 너비 우선 탐색 ↩︎ ↩︎² ↩︎³

4. n-ary Tree는 degree의 최대 수가 n인 tree를 의미하며, 모든 노드가 n개를 초과하는 자식 노드를 가지지 않는 트리라고도 정의한다. ↩︎